prawdopodobieństwo warunkowe biedrona: W czasie lotu z Warszawy do Auckland pasażerowie trzykrotnie zmieniają samolot. Prawdopodobieństwa zaginięcia bagażu w trzech kolejnych miejscach przesiadki wynoszą odpowiednio: 40%, 20% i 10%. W Auckland okazało się że mój bagaż nie dotarł ze mną do miejsca przeznaczenia. Jakie jest prawdopodobieństwo, że utknął w drugim z portów lotniczych? Proszę o pomoc.z góry dziękuję

Staszek: żeby zgubić się w 2 miejscu trzeba się zgubić w ogóle więc jakie jest prawdopodobieństwo że zgubiliśmy się akurat na 2 przesiadce? (gdy wiemy że zgubiliśmy się na pewno)

	0,2
P=		=27=0,2857
	0,4+0,2+0,1

Staszek: W moim rozumowaniu wkradł się błąd prawdopodobieństwo zgubienia bagażu 1 raz to i owszem 40% , ale p. zgubienia bagażu 2 raz jest możliwe gdy udało mu sie nie zgubić za 1 razem p.1 = 0,4 p.2 =(1−0,4)*0,2=0,12 p.3 =((1−0,4)*0,2)*0,1=0,12*0,1=0,012 p1+p2+p3=0,532

	0,2
czyli P=		=0,20,532=0,3759
	0,4+0,12+0,012

SP: Na moje ok w p.3 powinno być (1−0,4)*(1−0,2)*0,1 no bo liczymy prawdopodobieństwo zaginięcia w każdym z miejsc, wiec w poprzednich nie mógł zaginąć ażeby zaginąć w p3. Dalszy tok rozumowania jest w porządku, tylko mianownik nam się nieco zmieni 0,4+0,12+0,048

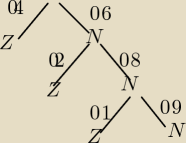
kylo1303: Nie do konca rozumiem dlaczego to zadanie jest tak zrobione. Moznaby rozrysowac drzewko: Z− zgubiony N− nie zgubnioy Tam wszedzie po 0 powinny byc przecinki. Wiec zeby zgubil sie w drugim miejscu, to w pierwszym musi byc okej, a w drugim juz zgubil. Sa to zdarzenia niezalezne wiec P(AnB)=P(A)*P(B) P(AnB)=0,6*0,2=0,12

kylo1303: Jednak to chyba nie sa zdarzenia niezalezne